BankConflict与WarpTiling

CUDA入门
20k 词

BankConflict介绍

基础概念

SM(Streathread tileg Multiprocessor)

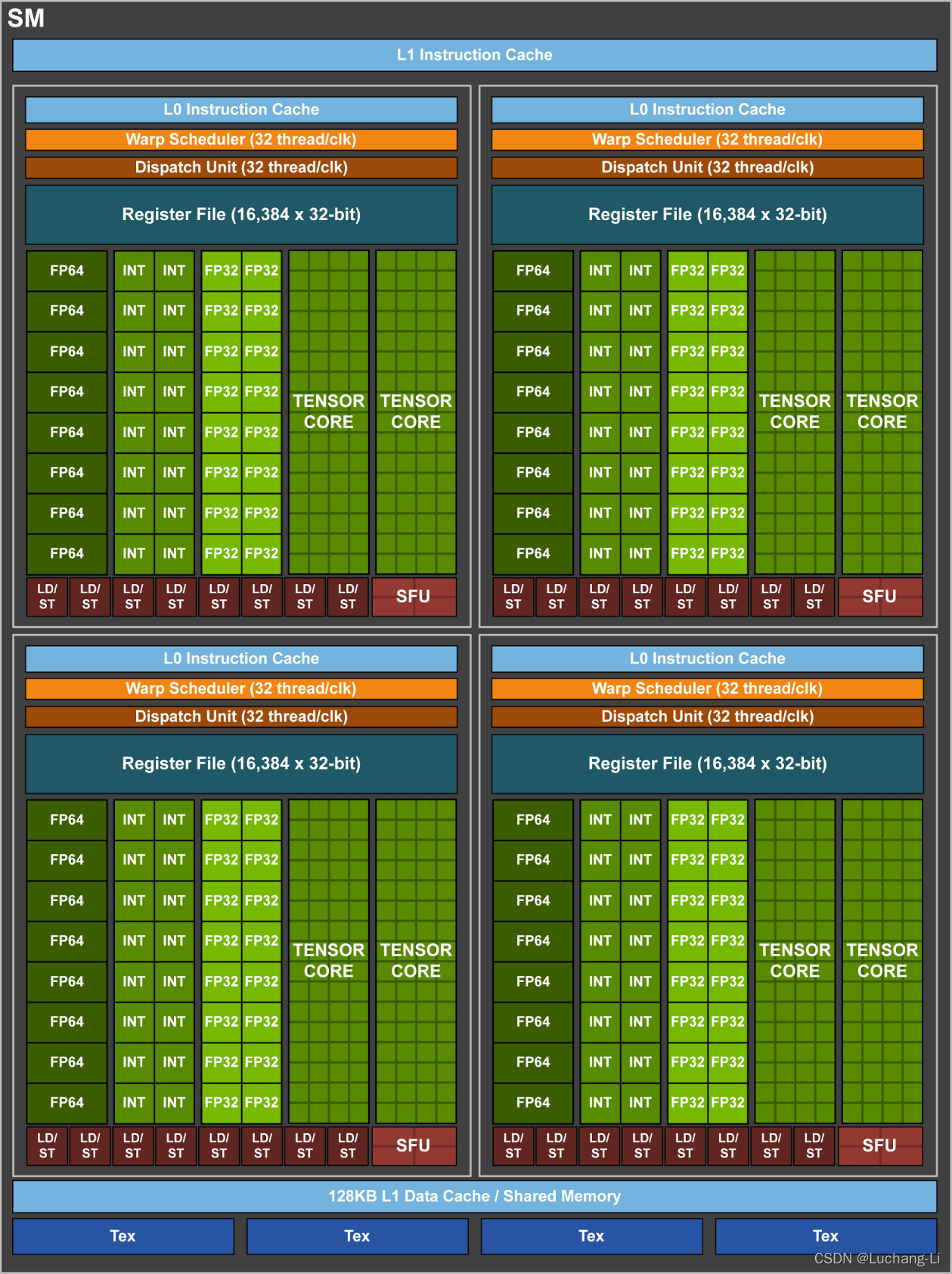
SM是CUDA编程模型中最核心的硬件计算单元之一，它负责实际调度和执行线程和线程束上的指令。

每个SM包含了多个硬件资源：

  • CUDA核心：执行浮点、整数运算的基础单元。
  • Warp Scheduler（Warp调度器）：调度和发射warp中的指令。
  • Register File（寄存器）：供线程临时存储数据。
  • Shared Memory（共享内存）：用于block内线程通信与快速数据缓存。
  • SFU（特殊功能计算单元）：计算 sin cos sqrt等复杂函数。
  • Load/Store 单元（LD/ST）：处理内存读写。
  • Tensor Core：用于矩阵乘法的高吞吐量计算单元。

下图是Volta GV100 Streathread tileg Multiprocessor (SM)的结构：

Volta GV100 Streathread tileg Multiprocessor (SM)

Shared Memory

位于GPU SM中的Shared Memory具有高速、低延迟的特性，是CUDA编程中非常重要的优化工具。

在CUDA编程中每个Block分配一块独立的Shared Memory，它可以被用于线程间通信、数据复用、缓存临时计算结果等场景。

每个SM的Shared Memory总量一般为48KB~128KB；在编程中要注意数据一致性。

GPU调度执行

  • SM调度单位为一个warp，每一个warp一般包含32个threads.
  • Shared Memory可以被一个Warp中的所有32个线程进行访问.

Bank

在CUDA的Shared Memory中，Bank是一种硬件组织方式，用以实现高带宽访问。

Shared Memory是按Bank划分的，每个Bank可以在一个时钟周期内为一个线程提供服务。

主流的NVIDIA GPU每个Shared Memory有32个Bank，每个Bank宽度为4B；这也就是说，每4B的地址对应一个Bank。

BankIdx=(address/4)%32BankIdx = (address/4)\%32

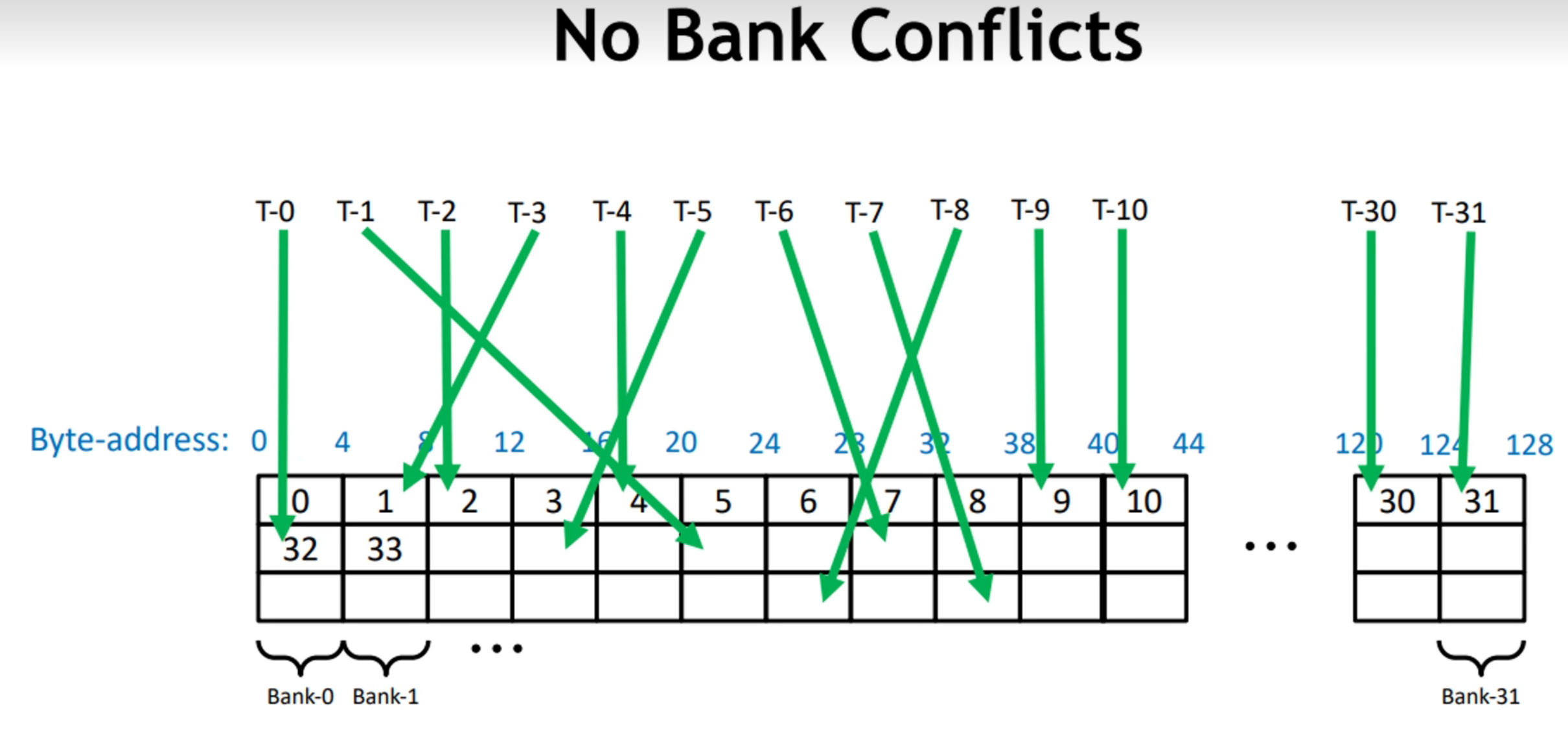
  • 当多个线程在同一个时钟周期下访问不同的bank，访问是并行的。
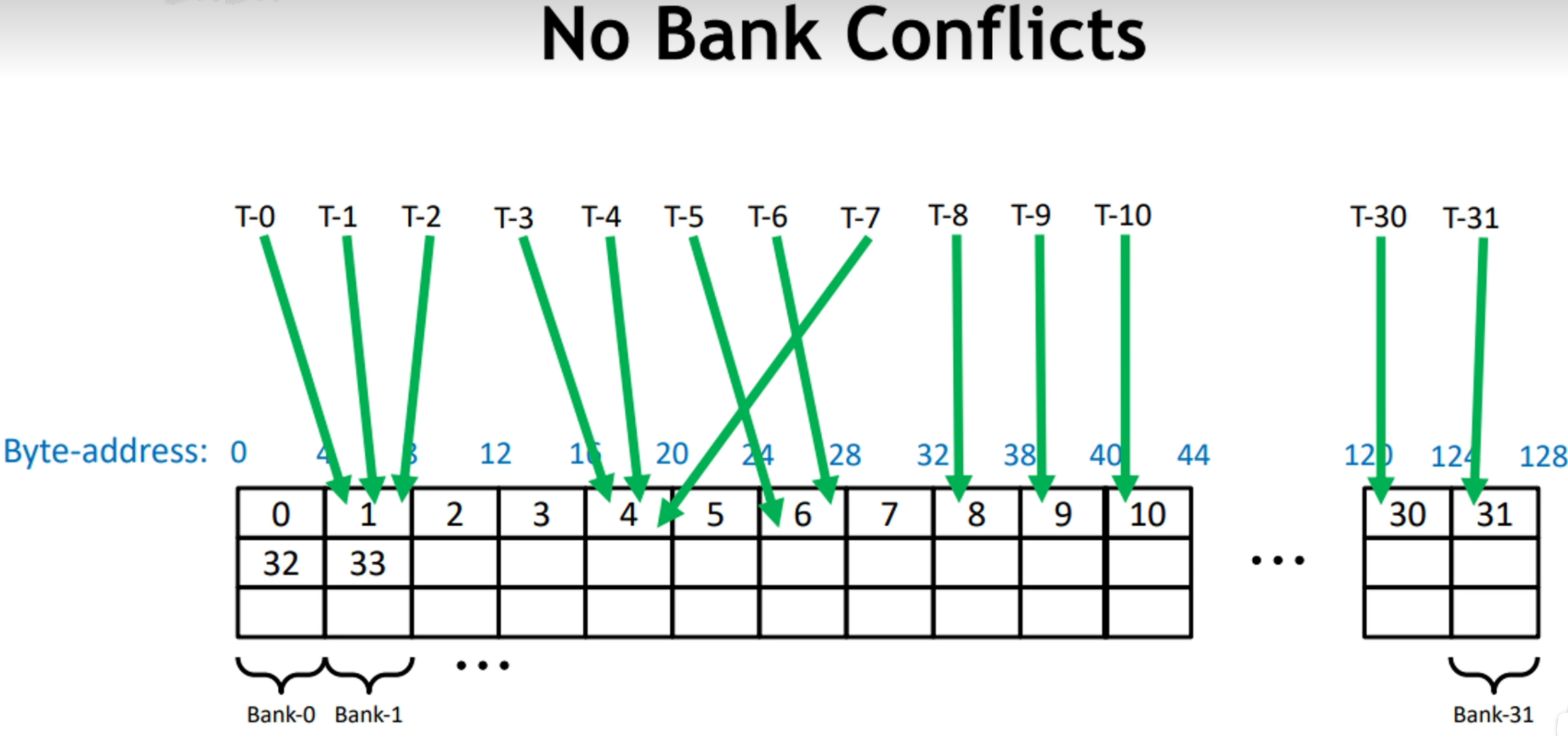
  • 当多个线程访问同一个bank的同一地址，将发生广播。
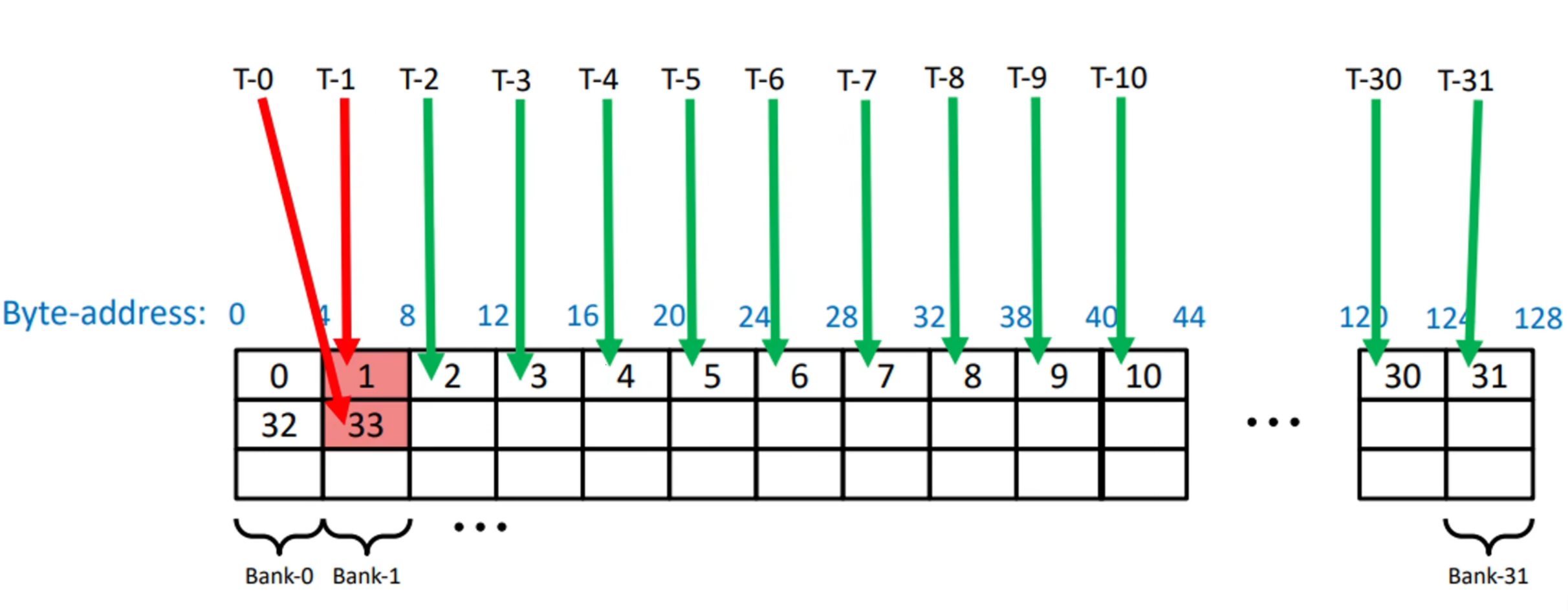
  • 当多个线程访问同一个bank的不同地址，访问将串行化。

什么是BankConflict

在Bank介绍中，我们说明了三种情况，分别是不同Bank并行访问、同一Bank同一地址广播、同一Bank不同地址串行；而BankConflict就是指第三种情况。

BankConflict是指在CUDA中使用共享内存时，同一个时钟周期内，多个线程访问同一个Bank内的不同地址时产生冲突。

无冲突情况

当多个线程在同一个时钟周期下访问不同的bank，访问是并行的：

NoBankConflict

其中，T-x指代thread-x，即说明线程的序号；绿色箭头指代了该线程访问的Bank；而每一个4B宽度的块，连续构成Bank0~Bank31，并循环往复，所以在图中，一列即为同一个Bank。

在该图中，虽然一个warp中的32个线程的访问并非按照连续地址进行，但是线程访问不同的Bank，该访问是可并行的。

当多个线程访问同一个bank的同一地址，将发生广播：

NoBankConflict2

此时，即使部分线程访问了同一个Bank，但是由于它们访问的地址是一致的，所以不会发生BankConflict.

冲突情况

当多个线程访问同一个bank的不同地址，访问将串行化：

BankConflict2

如图所示，T-0 T-1线程同时访问了Bank-1，但前者访问4-8，后者访问132-136，发生了2-way Bank Conflict.

x-way指代了Bank Conflict的冲突等级，最高可达32-way Bank Conflict，即一个warp中的线程同时访问同一个Bank中的不同地址。

发生Bank Conflict时，会严重降低共享内存带宽，导致吞吐量下降；此外，冲突造成性能波动大，难以debug.

案例分析

冲突在哪

在上一节，我们提供了基础的矩阵乘法优化代码，部分代码如下：

1
2
3
4
5
6
7
8
9
\\ 配置参数
const int BM = 128;
const int BN = 128;
const int BK = 8;
const int TM = 8;
const int TN = 8;
\\ 计算线程对应该块计算的C块中的起始行列
const uint threadRow = threadIdx.x / (BN / TN);
const uint threadCol = threadIdx.x % (BN / TN);

由于BN/TN=16BN/TN=16，这说明在一个warp中，前16个线程与后16个线程分别具有相同的threadRow；每16个线程为一个周期，分别具有0，1，…，15的threadCol.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
for (int blkIdx = 0; blkIdx < K; blkIdx += BK)
{
    /**载入共享内存**/

    __syncthreads();

    A += BK;
    B += BK * N;

    for (uint dotIdx = 0; dotIdx < BK; ++dotIdx)
    {
        for (int i = 0; i < TM; i++)
        {
            regM[i] = As[dotIdx * BM + threadRow * TM + i];
        }
        for (int i = 0; i < TN; i++)
        {
            regN[i] = Bs[dotIdx * BN + threadCol * TN + i];
        }

        for (uint resIdxM = 0; resIdxM < TM; ++resIdxM)
        {
            for (uint resIdxN = 0; resIdxN < TN; ++resIdxN) 
            {
                threadResults[resIdxM * TN + resIdxN] += regM[resIdxM] * regN[resIdxN];
            }
        }
    }
    __syncthreads();
}

其中，将共享内存数据载入寄存器时：

对As访问dotIdx * BM + threadRow * TM + i（在A加载进共享内存时，对A进行了转置），若dotIdx与i不变，那么同一个warp前16个线程访问dotIdx * BM + 0 * TM + i，访问同一地址，不发生冲突，后16个线程访问dotIdx * BM + 1 * TM + i，也访问同一地址，也不冲突；前后访问地址相差TM即8个float，32B；即前后地址相差8个Bank的宽度，仍在32个Bank范围内，不会发生Bank Conflict.

对Bs访问dotIdx * BN + threadCol * TN + i，若dotIdx与i不变，一致从第一个线程开始的16个线程中，相邻线程的threadCol相差1（0，1，…，15），则每俩线程访问地址相差一个TNfloat，即8float，即32B。从0号线程到3号线程，相差32float，即128B，恰好为一轮32个Bank；那么threadIdx每相差4（例如，0号线程与4号线程）就会产生一个Bank Conflict.

Warp Tiling

我们先考虑做了什么，再考虑为什么这么做。在这里我们重点关注从共享内存读取到寄存器时发生的Bank Conflict，其余的Bank Conflict也会写在文中。

以下为本次Warp Tiling实现的参数设置，可以截图放在旁边。

1
2
3
4
5
6
7
8
const uint BN = 128;
const uint BM = 64;
const uint BK = 8;
const uint WN = 64;
const uint WM = 32;
const uint WNITER = 2;
const uint TN = 4;
const uint TM = 4;

从全局内存载入共享内存

在载入共享内存之前（或者说在遍历K之前），我们需要对A B C指针进行移动，使其移动到指定的形状分别为[BM, BK] [BK, BN] [BM, BN]的块起始位置。
移动参考：

1
2
3
4
5
const uint cRow = blockIdx.y;
const uint cCol = blockIdx.x;

A += cRow * BM * K;
B += cCol * BN;

对A矩阵，需要纵向移动cRow个[BM, Bk]块，之后的行遍历按BK大小间隔遍历K，那么总共需要移动cRow * BM行，共cRow * BM * K个数据。

对B矩阵，需要横向移动cCol个[BK, BN]块，之后的列遍历按BK大小间隔遍历K，所以总共横向移动cCol * BN列，共cCol * BN * 1个数据。

PS：在这里我们先不介绍C指针如何移动，首先从A B矩阵读入不需要C；其次，再介绍完各种块的层次后再介绍C指针更为合适。

A矩阵

在本节，我们关注一个Block中的所有线程，是如何将(BM, BK)大小的A矩阵块向量化并转置载入共享内存的。

我们会使用float4读取全局内存至寄存器，再将寄存器转置载入到共享内存，也就是说每个线程一次负责4个数据的载入。

那么，我们首先就要确认从哪个起点开始载入连续的4个数据。

1
2
3
const uint innerRowA = threadIdx.x / (BK / 4);
const uint innerColA = threadIdx.x % (BK / 4);
constexpr uint rowStrideA = (NUM_THREADS * 4) / BK;

在行主序的A矩阵中，以四个数据为一组，每行有BK/4组，所以每个线程的行起点为threadIdx.x / (BK / 4)，而列起点为threadIdx.x % (BK / 4).

考虑到线程数目的四倍不一定恰好是(BM, BK)大小矩阵的数据量，所以需要引入偏移量，满足少量的A矩阵块的溢出需求，即部分线程可能额外读取。

那么每个线程都读取一次数据，一个Block总共读取(NUM_THREADS * 4)，读取(NUM_THREADS * 4) / BK行。那么同一个线程，如果第二次读取全局内存，下次读取的数据的行将(NUM_THREADS * 4) / BK作为0行，即读取第(NUM_THREADS * 4) / BK + innerRowA行。

明白了这些数据，我们便能很快写出读入A矩阵某块进入共享内存的代码：

1
2
3
4
5
6
7
8
for (uint offset = 0; offset + rowStrideA <= BM; offset += rowStrideA) {
    const float4 tmp = reinterpret_cast<const float4 *>(
        &A[(innerRowA + offset) * K + innerColA * 4])[0];
    As[(innerColA * 4 + 0) * BM + innerRowA + offset] = tmp.x;
    As[(innerColA * 4 + 1) * BM + innerRowA + offset] = tmp.y;
    As[(innerColA * 4 + 2) * BM + innerRowA + offset] = tmp.z;
    As[(innerColA * 4 + 3) * BM + innerRowA + offset] = tmp.w;
}

B矩阵

B矩阵与A矩阵思路类似，但是不需要转置。

1
2
3
4
5
6
7
8
9
10
const uint innerRowB = threadIdx.x / (BN / 4);
const uint innerColB = threadIdx.x % (BN / 4);
constexpr uint rowStrideB = NUM_THREADS / (BN / 4);

for (uint offset = 0; offset + rowStrideB <= BK; offset += rowStrideB) {
    reinterpret_cast<float4 *>(
        &Bs[(innerRowB + offset) * BN + innerColB * 4])[0] =
        reinterpret_cast<const float4 *>(
            &B[(innerRowB + offset) * N + innerColB * 4])[0];
}

Bank Conflict!!!

在读取A矩阵时，存在BankConflict.

我们假设有1threadIdx.x = 0, 11两个线程，它们共处于一个warp，满足同一warp的线程的条件。

thread-0对应的innerColA = 0，thread-1对应的innerColA = 1，二者的innerRowA = 0.

在读取As[(innerColA * 4 + 0) * BM + innerRowA + offset]，thread-0读取As[(0 * 4 + 0) * BM + 0 + offset]，thread-1读取As[(1 * 4 + 0) * BM + 0 + offset]。

通过上述两个例子，我们很容易理解以BK/4为一组，组内相邻的两个线程对应的innerColA是连续的，地址是固定差4BM的。

共享内存地址被 按 4 字节（float）划分 bank 编号：

1
bank = address_in_float % 32

你访问的地址As[(innerColA * 4 + 0) * BM + innerRowA + offset]为As[innerColA * 4 * 64 + innerRowA + offset].

当 innerColA 连续变化时，innerColA * 512 也连续变化，但：

1
2
3
4
(0 * 256 + innerRowA + offset) % 32 = (innerRowA + offset) % 32
(1 * 256 + innerRowA + offset) % 32 = (innerRowA + offset) % 32
(2 * 256 + innerRowA + offset) % 32 = (innerRowA + offset) % 32
...

所以不同线程访问的地址都映射到 bank (innerRowA + offset) % 32，产生Bank Conflict.

矩阵层次与变量名

我们已经成功将A矩阵中(BM, BK)大小的块和B矩阵中(BK, BN)大小的块载入到共享内存中，现在我们需要思考，如何从共享内存取出合适的数据塞入寄存器，再通过寄存器的数据完成计算。

在这里，我们将梳理具体的矩阵层次，明确每个变量的具体含义。

我们以C矩阵的划分为例。

最小单位矩阵

大小为(TM, TN)的块是计算的最小单位。我在这里使用thread tile指代它。

在本例中thread tile块为（4，4）大小。

一个warp处理的矩阵

32个thread tile组成矩阵，包含数据量为32*TM*TN。它的形状，即长宽由上层决定，我在这里使用warp sub tile指代该矩阵。

在本例中warp sub tile由（4，4）大小的thread tile组成，总共包含32*4*4个数据总额。

由warp sub tile构成的小块

我在这里用warp tile指代它，描述该块包含多个变量名：

  • WM：该块的行数，人为设置。
  • WN：该块的列数，人为设置。
  • WNITER: 一行有WNITER个warp sub tile，在本例中是人为设置得到的。
  • WMITER：一列有WMITER个warp sub tile，WMITER = (WM * WN) / (WARPSIZE * TM * TN * WNITER).
  • WSUBM：描述了warp sub tile的具体行数，WSUBM = WM / WMITER.
  • WSUBN：描述了warp sub tile的具体列数，WSUBN = WN / WNITER.

在本例中，WNITER人为设置为2，WMITER计算得到为2，说明一个warp tile包含（2，2）个wap sub tile.

每个wap sub tile的行数为WSUBM，即32行；列数为WSUBN，即16列。

此时我们可以反推warp sub tile的组成，已知每个最小块为（4，4），所以warp sub tile是由（8，4）个thread tile组成的。

回顾warp sub tile

为了将threadIdx映射到warp sub tile，便于从共享内存并行写入寄存器，我们计算以下变量：

  • threadIdxInWarp：将threadIdx映射到[0,31]，对应一个warp sub tile中的32个thread tile块的序号，threadIdxInWarp = threadIdx.x % WARPSIZE.
  • threadColInWarp：使用threadIdx计算该序号位于warp sub tile中的哪一列，threadColInWarp = threadIdxInWarp % (WSUBN / TN).
  • threadRowInWarp：使用threadIdx计算该序号位于warp sub tile中的哪一行，threadRowInWarp = threadIdxInWarp / (WSUBN / TN).

由warp tile组成的矩阵

该矩阵由(WM, WN)大小的warp tile组成，该矩阵形状为(BM, BN)，我们称为block tile.

这说明：该矩阵包含(BM/WM, BN/WN)个warp tile.

在本例中，该矩阵形状为(128, 64)，包含(2, 2)个warp tile.

回顾warp tile

为了将线程映射到不同的warp tile，提出以下变量：

  • warpIdx：线程映射到warpIdx的warp tile，warpIdx = threadIdx.x / WARPSIZE.
  • warpCol：指定序号的warp tile在block tile第warpCol列，warpCol = warpIdx % (BN / WN).
  • warpRow：指定序号的warp tile在block tile第warpRow行，warpRow = warpIdx / (BN / WN).

由block tile构成最终的C

block tile按照blockIdx进行映射，共同构成(M, N)大小的矩阵。我们可以叫做grid tile.

  • cRow：在C中第cRow行block tile. cRow = blockIdx.y.
  • cCol：在C中第cCol列block tile. cCol = blockIdx.x.

C指针移动

对于C矩阵，它同样先需要移动到指定的block tile块，即C += cRow * BM * N + cCol * BN。

但是本次实现采用warp tiling，一个block包含多个warp，每个warp单独实现一个warp tile，所以需要根据当前的threadIdx在[BM, BN]块中找到对应的warp块，根据计算得到的对应warpIdx所在的行列，单论warp tile相对所在block tile的位置，向下占warpRow * WM行，向右占warpCol * WN列。

计算纵向总行数为：cRow * BM + warpRow * WM，总数据个数为：(cRow * BM + warpRow * WM) * N；横向总列数为：cCol * BN + warpCol * WN.

1
2
3
4
const uint cRow = blockIdx.y;
const uint cCol = blockIdx.x;

C += (cRow * BM + warpRow * WM) * N + cCol * BN + warpCol * WN;

从共享内存载入到寄存器

我们介绍完了各个矩阵的层次，接下来将介绍在计算前，如何将数据从As载入到regM中。

最外层循环如下：

1
2
3
4
for (uint dotIdx = 0; dotIdx < BK; ++dotIdx)
{
    /* 载入寄存器，并计算 */
}

在单次循环中，每个线程要从As中载入WMITER个的TM块，从Bs中载入WNITER个的TN块，以进行后续的计算。

As矩阵

需谨记，As是一个经过转置的矩阵，A矩阵一个block tile形状为(BM, BK)，在As中则为(BK, BM).

所以数学意义上，单次dotIdx，我们应该取A的列（内存地址连续），但实际上我们取的是沿着BM方向的行中的WMITER*TM个数据。

在BM方向上，首先需要确定在(BK, BM)块中哪一行开始的，这有dotIdx决定，dotIdx遍历BK，即遍历block tile的每一行。

那么起始点在：dotIdx * BM.

考虑block tile层次的移动：在block tile的组成单位是warp tile，每个block形状为(WM, WN)，转置后为(WN, WM). thread的行序号为warpRow，转置后列序号为warpRow，代表该行第warpRow个的warp tile.

那么起始点应该以WM为一组，前进warpRow次，即增加warpRow * WM. 目前序号来到：dotIdx * BM + warpRow * WM.

在warp tile的下一层是warp sub tile，每个warp sub tile的形状为(WSUBM, WSUBN)，转置后为(WSUBN, WSUBM)一个warp tile包含(WMITER, WNITER)个warp sub tile，转置后形状为(WNITER, WMITER).

为了载入WMITER个的TM块，这里有一层循环，遍历WMITER，并根据当前WMITER的序号，前进相应的WSUBM倍。

1
2
3
4
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx)
{
    // 目前序号来到了dotIdx * BM + warpRow * WM + wSubRowIdx * WSUBM
}

在warp sub tile的下一层，是thread tile，形状为(TM, TN)，转置后为(TN, TM)，warp sub tile由(WSUBM/TM, WSUBN/TN)个thread tile组成，转置后也就是说我们需要明确，当前thread在哪列thread tile中，这里需要用到threadRowInWarp = threadIdxInWarp / (WSUBN / TN)，序号应继续前进threadRowInWarp * TM.

恭喜，我们已经完全确定了该次循环的读取起点，我们只需要遍历该起点开始的TM个数据即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int idx = 0;

idx += dotIdx * BM;

idx += warpRow * WM;

for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx)
{
    float tmpIdx = idx + wSubRowIdx * WSUBM;

    tmpIdx += threadRowInWarp * TM;

    for (uint i = 0; i < TM; ++i)
    {
        regM[wSubRowIdx * TM + i] =
              As[tmpIdx + i];
    }

}

代码整理后为：

1
2
3
4
5
6
7
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
        for (uint i = 0; i < TM; ++i) {
          regM[wSubRowIdx * TM + i] =
              As[dotIdx * BM + warpRow * WM + wSubRowIdx * WSUBM +
                 threadRowInWarp * TM + i];
        }
}

Bs矩阵

Bs矩阵形状为(BK, BN)，在这里我们同样按照行取。
思路比As矩阵个人觉得还要简单，因为没有转置，以下是概述。

首先根据dotIdx确定起点：dotIdx * BN.

在block tile部分，处理组成单位warp tile，增加warpCol个长度，长度为WN.

所以序号更新为dotIdx * BN + warpCol * WN.

后续的内容与As矩阵思路一致，遍历warp sub tile，在warp sub tile中确定第几个thread tile块开始。

代码如下：

1
2
3
4
5
6
7
for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
        for (uint i = 0; i < TN; ++i) {
          regN[wSubColIdx * TN + i] =
              Bs[dotIdx * BN + warpCol * WN + wSubColIdx * WSUBN +
                 threadColInWarp * TN + i];
        }
}

为什么读共享内存不会出现Bank Conflict

我们从threadIdx入手，BankConflict只发生在一组warp中threadIdx连续的32个线程间。

在block tile划分warp tile时，我们先计算了warpIdx = threadIdx.x / WARPSIZE，将线程划分到不同的warp tile去，不同warp tile属于不同的warp管理，它们之间的访问不会出现Bank Confict.

我们只需要单独考虑每个warp tile读取时，是否会出现bank conflict.

以As矩阵为例，假设dotIdx i wSubRowIdx不变，同一个warp tile的warpRow也相同，一个时钟周期，访问的差异在于threadRowInWarp * TM.

已知：
threadIdxInWarp = threadIdx.x % WARPSIZE
threadRowInWarp = threadIdxInWarp / (WSUBN / TN)

同一个warpblock中的Idx为连续的0~31；WSUBN/TN为8

所以threadRowInWarp的范围框定在了0~3之间。

以0号warp中的0~31号线程为例：

1
2
3
4
T0~7 -> dotIdx * BM + warpRow * WM + wSubRowIdx * WSUBM + 0 * TM + i
T8~15 -> dotIdx * BM + warpRow * WM + wSubRowIdx * WSUBM + 1 * TM + i
...
T24~31-> dotIdx * BM + warpRow * WM + wSubRowIdx * WSUBM + 3 * TM + i

首位访问地址相差3*TM个float即12个float，小于一个bank的宽度。

所在warp在访问As矩阵时，不存在Bank冲突。

以Bs矩阵为例，假设dotIdx i wSubRowIdx不变，同一个warp tile的warpRow也相同，一个时钟周期，访问的差异在于threadColInWarp * TN.

已知：threadIdxInWarp = threadIdx.x % WARPSIZE threadColInWarp = threadIdxInWarp % (WSUBN / TN)

同一个warpblock中的Idx为连续的0~31；WSUBN/TN为8

所以threadColInWarp的范围框定在了0~7之间。

以0号warp中的0~31号线程为例：

1
2
3
4
T0, 8, 16, 24 -> dotIdx * BN + warpCol * WN + wSubColIdx * WSUBN + 0 * TN + i
T1, 9, 17, 25 -> dotIdx * BN + warpCol * WN + wSubColIdx * WSUBN + 1 * TN + i
...
T7, 15, 23, 31 -> dotIdx * BN + warpCol * WN + wSubColIdx * WSUBN + 7 * TN + i

首位访问地址相差7*TM个float即28个float，小于一个bank的宽度。

所在warp在访问Bs矩阵时不存在Bank冲突。

移动指针

在计算之前我们需要对A，B指针进行位移，以确保下一次循环，A，B指针从正确的位置开始：

1
2
A += BK;
B += BK * N;

计算

在这里，我们以TM，TN的外积为一组，进行WMITER*WNITER次计算。

所以我们临时存储计算结果的寄存器是(WMITER*TM, WNITER*TN)形状的.

我们在外围进行了两层循环，分别遍历WMITER和WNITER:

1
2
3
4
5
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
        for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
            ...
    }
}

接下来介绍如何使用分配的寄存器。

首先我们考虑现在寄存器写入哪一行：

对于当前遍历的wSubRowIdx，前有wSubRowIdx * TM，在本轮(TM, TN)块中，处于resIdxM行，所以行为wSubRowIdx * TM + resIdxM，行的起始序号为(wSubRowIdx * TM + resIdxM) * (WNITER * TN).

接下来考虑该行第几列，首先是在(WMITER, WNITER)块中，处于wSubColIdx列，序号应加上wSubColIdx * TN，在(TM, TN)块中处于resIdxN.

所以序号最终为：(wSubRowIdx * TM + resIdxM) * (WNITER * TN) + (wSubColIdx * TN) + resIdxN.

计算代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
        for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
          for (uint resIdxM = 0; resIdxM < TM; ++resIdxM) {
            for (uint resIdxN = 0; resIdxN < TN; ++resIdxN) {
              threadResults[(wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                            (wSubColIdx * TN) + resIdxN] +=
                  regM[wSubRowIdx * TM + resIdxM] *
                  regN[wSubColIdx * TN + resIdxN];
            }
        }
    }
}

输出至C矩阵

在计算完成后，我们需要将(WMITER*TM, WNITER*TN)形状的寄存器中的计算结果搬运至C矩阵中。

在这里，我们同样采用向量化的方式搬运数据。

首先，与计算时读入寄存器一样，我们需要两个循环遍历每一个warp sub tile中的结果。

1
2
3
4
5
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
    for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
        ...
    }
}

在前文中，我们已经将C指针移动到了指定block tile中的指定warp tile，现在只用考虑warp tile内部的对应关系，即warp sub tile块。

warp tile包含[WMITER, WNITER]个warp sub tile，每个块为[WSUBM, WSUBN]大小。

所以C矩阵在指定warp tile起点的基础上，向下移动uSubRowIdx * WSUBM行，即移动(wSubRowIdx * WSUBM) * N个数据，向右移动wSubColIdx * WSUBN列。

所以本轮等待被输入的C矩阵的起点在：C + (wSubRowIdx * WSUBM) * N + wSubColIdx * WSUBN.

那么C指针可表示为：

1
float *C_interim = C + (wSubRowIdx * WSUBM) * N + wSubColIdx * WSUBN;

为了提高传输效率，同样使用向量化加载，一次加载float4类型的数据，即一次加载4个float的数据。

所以在内层的循环如下：

1
2
3
4
5
for (uint resIdxM = 0; resIdxM < TM; resIdxM += 1) {
    for (uint resIdxN = 0; resIdxN < TN; resIdxN += 4){
        ...
    }
}

C指针还要再以thread tile块为单位进行移动，以计算处于threadthread tile中的哪个thread tile。

还记得threadRowInWarp和threadColInWarp吗，它是thread在单个threadthread tile所指向的thread tile块的行列。

所以C指针还需要向下移动threadRowInWarp * TM，向右移动threadColInWarp * TN，最终到达C + threadRowInWarp * TM * N + threadColInWarp * TN.

现在我们终于来到了本线程本轮循环中将要输入的thread tile块的起始位置！！！

内层循环给了我们thread tile块内部的行列(resIdxM, resIdxN)，所以C指针还要再向下移动resIdxM行，向右移动resIdxN列，现在C指针来到了：C + threadRowInWarp * TM * N + threadColInWarp * TN + resIdxM * N +resIdxN.

1
C_interim[(threadRowInWarp * TM + resIdxM) * N + threadColInWarp * TN + resIdxN])[0]

为使用float4指针批量读取：

1
2
float4 tmp = reinterpret_cast<float4 *>(
    &C_interim[(threadRowInWarp * TM + resIdxM) * N + threadColInWarp * TN + resIdxN])[0];

我们将四个数据批量从全局内存载入寄存器。

遍历寄存器threadResults的序号计算方式与上一节完全一致，同样使用：(wSubRowIdx * TM + resIdxM) * (WNITER * TN) + (wSubColIdx * TN) + resIdxN.

那么读取四个数据并计算的代码如下：

1
2
3
4
5
const int i = (wSubRowIdx * TM + resIdxM) * (WNITER * TN) + wSubColIdx * TN + resIdxN;
tmp.x = alpha * threadResults[i + 0] + beta * tmp.x;
tmp.y = alpha * threadResults[i + 1] + beta * tmp.y;
tmp.z = alpha * threadResults[i + 2] + beta * tmp.z;
tmp.w = alpha * threadResults[i + 3] + beta * tmp.w;

完成计算后，我们再批量写会处于全局内存的C矩阵：

1
2
reinterpret_cast<float4 *>
(&C_interim[(threadRowInWarp * TM + resIdxM) * N + threadColInWarp * TN + resIdxN])[0] = tmp;

输出结果的总代码可见：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
        for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
        float *C_interim = C + (wSubRowIdx * WSUBM) * N + wSubColIdx * WSUBN;
        for (uint resIdxM = 0; resIdxM < TM; resIdxM += 1) {
            for (uint resIdxN = 0; resIdxN < TN; resIdxN += 4) {
            float4 tmp = reinterpret_cast<float4 *>(
                &C_interim[(threadRowInWarp * TM + resIdxM) * N +
                            threadColInWarp * TN + resIdxN])[0];
            const int i = (wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                            wSubColIdx * TN + resIdxN;
            tmp.x = alpha * threadResults[i + 0] + beta * tmp.x;
            tmp.y = alpha * threadResults[i + 1] + beta * tmp.y;
            tmp.z = alpha * threadResults[i + 2] + beta * tmp.z;
            tmp.w = alpha * threadResults[i + 3] + beta * tmp.w;
            reinterpret_cast<float4 *>(
                &C_interim[(threadRowInWarp * TM + resIdxM) * N +
                            threadColInWarp * TN + resIdxN])[0] = tmp;
            }
        }
    }
}

总体代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <cassert>
#include <cstdio>
#include <cstdlib>
#include <cublas_v2.h>
#include <cuda_runtime.h>

typedef unsigned int uint;

const int M = 2048;
const int N = 2048;
const int K = 4096;
float alpha = 1.0f;
float beta = 0.5f;
const int ITER = 1000;

#define CEIL_DIV(M, N) (((M) + (N)-1) / (N))
const int WARPSIZE = 32;
const uint NUM_THREADS = 128;

const uint BN = 128;
const uint BM = 64;
const uint BK = 8;
const uint WN = 64;
const uint WM = 32;
const uint WNITER = 2;
const uint TN = 4;
const uint TM = 4;

template <const int BM, const int BN, const int BK, const int WM, const int WN,
    const int WNITER, const int TM, const int TN, const int NUM_THREADS>
__global__ void __launch_bounds__(NUM_THREADS)
sgemmWarptiling(int M, int N, int K, float alpha, float* A, float* B,
    float beta, float* C) {
    const uint cRow = blockIdx.y;
    const uint cCol = blockIdx.x;
    A += cRow * BM * K;
    B += cCol * BN;
 
    const uint warpIdx = threadIdx.x / WARPSIZE; 
    const uint warpCol = warpIdx % (BN / WN);
    const uint warpRow = warpIdx / (BN / WN);
    C += (cRow * BM + warpRow * WM) * N + cCol * BN + warpCol * WN;

    constexpr uint WMITER = (WM * WN) / (WARPSIZE * TM * TN * WNITER);
    constexpr uint WSUBM = WM / WMITER;
    constexpr uint WSUBN = WN / WNITER;


    const uint threadIdxInWarp = threadIdx.x % WARPSIZE;        
    const uint threadColInWarp = threadIdxInWarp % (WSUBN / TN);
    const uint threadRowInWarp = threadIdxInWarp / (WSUBN / TN);

    __shared__ float As[BM * BK];
    __shared__ float Bs[BK * BN];

    const uint innerRowA = threadIdx.x / (BK / 4);
    const uint innerColA = threadIdx.x % (BK / 4);
    constexpr uint rowStrideA = (NUM_THREADS * 4) / BK;
    const uint innerRowB = threadIdx.x / (BN / 4);
    const uint innerColB = threadIdx.x % (BN / 4);
    constexpr uint rowStrideB = NUM_THREADS / (BN / 4);

    float threadResults[WMITER * TM * WNITER * TN] = { 0.0 };

    float regM[WMITER * TM] = { 0.0 };
    float regN[WNITER * TN] = { 0.0 };

   
    for (uint bkIdx = 0; bkIdx < K; bkIdx += BK) {
        for (uint offset = 0; offset + rowStrideA <= BM; offset += rowStrideA) {
            float4 tmp = reinterpret_cast<float4*>(
                &A[(innerRowA + offset) * K + innerColA * 4])[0];
            As[(innerColA * 4 + 0) * BM + innerRowA + offset] = tmp.x;
            As[(innerColA * 4 + 1) * BM + innerRowA + offset] = tmp.y;
            As[(innerColA * 4 + 2) * BM + innerRowA + offset] = tmp.z;
            As[(innerColA * 4 + 3) * BM + innerRowA + offset] = tmp.w;
        }

        for (uint offset = 0; offset + rowStrideB <= BK; offset += rowStrideB) {
            reinterpret_cast<float4*>(
                &Bs[(innerRowB + offset) * BN + innerColB * 4])[0] =
                reinterpret_cast<float4*>(
                    &B[(innerRowB + offset) * N + innerColB * 4])[0];
        }
        __syncthreads();

        for (uint dotIdx = 0; dotIdx < BK; ++dotIdx) {
            for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
                for (uint i = 0; i < TM; ++i) {
                    regM[wSubRowIdx * TM + i] =
                        As[(dotIdx * BM) + warpRow * WM + wSubRowIdx * WSUBM +
                        threadRowInWarp * TM + i];
                }
            }
            for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
                for (uint i = 0; i < TN; ++i) {
                    regN[wSubColIdx * TN + i] =
                        Bs[(dotIdx * BN) + warpCol * WN + wSubColIdx * WSUBN +
                        threadColInWarp * TN + i];
                }
            }

            for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
                for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
                    for (uint resIdxM = 0; resIdxM < TM; ++resIdxM) {
                        for (uint resIdxN = 0; resIdxN < TN; ++resIdxN) {
                            threadResults[(wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                                (wSubColIdx * TN) + resIdxN] +=
                                regM[wSubRowIdx * TM + resIdxM] *
                                regN[wSubColIdx * TN + resIdxN];
                        }
                    }
                }
            }
        }
        A += BK;    
        B += BK * N; 
        __syncthreads();
    }

    for (uint wSubRowIdx = 0; wSubRowIdx < WMITER; ++wSubRowIdx) {
        for (uint wSubColIdx = 0; wSubColIdx < WNITER; ++wSubColIdx) {
            float* C_interim = C + (wSubRowIdx * WSUBM) * N + wSubColIdx * WSUBN;
            for (uint resIdxM = 0; resIdxM < TM; resIdxM += 1) {
                for (uint resIdxN = 0; resIdxN < TN; resIdxN += 4) {
                    float4 tmp = reinterpret_cast<float4*>(
                        &C_interim[(threadRowInWarp * TM + resIdxM) * N +
                        threadColInWarp * TN + resIdxN])[0];
                    const int i = (wSubRowIdx * TM + resIdxM) * (WNITER * TN) +
                        wSubColIdx * TN + resIdxN;
                    tmp.x = alpha * threadResults[i + 0] + beta * tmp.x;
                    tmp.y = alpha * threadResults[i + 1] + beta * tmp.y;
                    tmp.z = alpha * threadResults[i + 2] + beta * tmp.z;
                    tmp.w = alpha * threadResults[i + 3] + beta * tmp.w;
                    reinterpret_cast<float4*>(
                        &C_interim[(threadRowInWarp * TM + resIdxM) * N +
                        threadColInWarp * TN + resIdxN])[0] = tmp;
                }
            }
        }
    }
}

int main()
{
    cudaError_t cudaStat;

    float* d_a, * d_b, * d_c;
    cudaMalloc((void**)&d_a, M * K * sizeof(float));
    cudaMalloc((void**)&d_b, K * N * sizeof(float));
    cudaMalloc((void**)&d_c, M * N * sizeof(float));

    cudaEvent_t start, end;
    cudaEventCreate(&start);
    cudaEventCreate(&end);

    cudaEventRecord(start);

    dim3 blockDim(NUM_THREADS);
    dim3 gridDim(CEIL_DIV(N, BN), CEIL_DIV(M, BM));

    for (int i = 0; i < ITER; i++)
    {
        sgemmWarptiling<BM, BN, BK, WM, WN, WNITER, TM,
            TN, NUM_THREADS>
            << <gridDim, blockDim >> > (M, N, K, alpha, d_a, d_b, beta, d_c);
    }
    cudaEventRecord(end);
    cudaEventSynchronize(end);

    float msec = 0.f;
    cudaEventElapsedTime(&msec, start, end);

    long long workfload = long long(M) * N * K * 2 * ITER;
    double avg_GFlops = (double(workfload) / 1e9) / (double(msec) / 1e3);
    printf_s("AveragePerformance %10.11f GFlops\n", avg_GFlops);

    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_c);
}

测试结果：9871.05248909252 GFlops

留言